Todella iso kiitos kaikille kyselyyn osallistuneille! Odotin kohtalaista suosiota some-jakojen ansiosta, mutta 147 vastausta ylitti odotukseni reippaasti, tämä blogi kun ei kävijämäärillä erityisesti voi retostella. Nyt esitän oman analyysini joistakin tuloksista; odotan mielenkiinnolla muiden havaintoja!
Päätavoitteena oli osoittaa, että ihmiset eivät ole niin satunnaisia. Siinä kysely onnistuikin: useampaan tehtävään kertyi vastauksia, jotka ovat kaukana satunnaisesta. Periaatteessa tätä voi hyödyntää, ja varmasti hyödynnetäänkin, ihmisiä vastaan. Toisin päin ajateltuna puolestaan oikeasti satunnaiset ilmiöt eivät ehkä tunnukaan meistä niin satunnaisilta. Ihminen on kehittynyt tunnistamaan kuvioita — sielläkin, missä niitä ei ole.
Kysely ei todellakaan täytä tieteellisiä standardeja. Otanta on varmasti kaukana satunnaisesta, koska kysely levisi enimmäkseen siitä kiinnostuneiden välityksellä. Lisäksi useammassa kysymyksessä oli epäonnistunut asettelu. Olen kuitenkin sitä mieltä, että virheiden analysointi on erinomainen tapa oppia, ja että ne siksi jopa sopivat tähän kevyeen kyselyyn. Mutta eiköhän siirrytä itse tuloksiin!
"Satunnaiset" luvut
Ensimmäisessä osiossa piti keksiä viisi satunnaista lukua väliltä 0–19. Tarkoituksena oli testata, suosivatko ihmiset kollektiivisesti tiettyjä lukuja. Oletuksenani oli, että parilliset luvut ja lukualueen ääripäät olisivat vähemmän suosittuja.
Itse asiassa niin ei käynytkään. Oheisella kuvaajalla näkyy lukujen jakauma koko tehtävässä, kun jokaista pitäisi olla keskimäärin 37 kappaletta. Ilmeisesti 4 ja 5 ovat lukujen supertähtiä, kun taas 14 ja 16 jäävät vähemmälle huomiolle. Parillisten ja parittomien jakauma on melko tasainen: 53 % luvuista oli parittomia. Ensimmäiseksi annetuissa luvuissa parittomien osuus oli huomattavasti suurempi, mutta loppua kohden ero tasoittui.
Kiinnostavana huomiona luvut ovat heikosti suuruusjärjestyksessä: keskimääräinen luku kasvaa kohta kohdalta. Tasaisimmin lukuja valittiin neljännessä kysymyksessä. Olisi myös kiinnostavaa tietää, miten jakauma muuttuu suuremmalla välillä. Varmistaakseni riittävän otoksen rajasin lukuvälin pieneksi — miten tapahtuisi vaikkapa välillä 0–100? Entä kuinka luvut jakautuvat yksilöllisesti, vaikkapa muutaman viikon varrella kerättynä?
"Satunnaiset" valinnat
Valintakysymyksistä ensimmäisessä piti valita yksi vaihtoehdoista 1–4. Numero 3 oli kansan ehdoton suosikki huikealla 42 % osuudella. Ovatko 1 ja 4 liian ääripäitä ja 2 parillisena vähemmän seksikäs keskimmäisistä vaihtoehdoista?
Toisessa satunnaisessa valinnassa kutakin ruutua ruksattiin käytännössä yhtä monta kertaa. Mitä puolestaan tulee ruksien määrään, niitä on odotettua enemmän. Miksikö — no esimerkiksi siksi, etten testannut nollan ruksin toimivuutta. Kuten varmasti jotkut huomasivat, "niin monta kuin haluat" tarkoittikin "miten vaan mutta ainakin yksi", koska olin epähuomiossa jättänyt kysymyksen pakolliseksi. Hupsistakeikkaa.
Ylivoimaisesti suosituin valinta oli kaikkien kohtien ruksaaminen. Myös rahapeleistä tutut kuviot 2, 3, 1+4 ja 2+3 olivat jokseenkin suosittuja, mutta eivät kovin suurella marginaalilla.
Kummallinen kolikonheitto
Kolikonheittotehtävässä minua kiinnosti nähdä, kuinka ihmiset välttelevät putkia, joissa sama puoli toistuu. Ihmiset yleensä katkaisevat putket lyhyeen, jotta tulos näyttäisi "satunnaisemmalta". Todellisuudessa pitkät putket ovatkin yleisempiä, joten ihmisen kädenjälki erottuu. Tässä datassa ilmiö todellakin toteutuu. Enintään kahden pituisia putkia on odotettua enemmän ja neljän tai viiden pituisia odotettua vähemmän.
Erilaisia kruuna-klaava-jonoja on $2^{6} = 64$ kappaletta, joten jokaista pitäisi olla pari-kolme kappaletta. Arvaatkin varmaan jo, kävikö niin. Peräti kolmasosa vastaajista aloitti jononsa "kruuna, kruuna, klaava, kruuna"! Toinen samankaltainen tulos näkyi datassa selvästi jo ensimmäisen päivän aikana. Ensimmäisistä heitoista 74 prosenttia oli kruunia (joka oli vasen vaihtoehto). Kannattanee siis luottaa ennemmin oikeaan kolikkoon.
Noutajan paino-ongelma
Tehtävä, jossa piti veikata koiran paino, pohjautuu 1800-luvun brittimatemaatikko sir Francis Galtonin kokeeseen. (Häneen on tutustuttu aiemmin tässä blogissa.) Galton teki kokeensa markkinoilla, joilla yleisö sai veikata näytteillä olevan härän painoa. Hän keräsi yleisön veikkaukset ja laski niistä keskiarvon ja mediaanin — kumpikin osui todella lähelle härän oikeaa painoa.
Tässä kyselyssä ei käynyt niin hyvin. Arvausten keskiarvo on 36,8 kiloa ja mediaani 34,0 kiloa. Keskihajonta on melkoisen valtava 15,4 — moni arvasi viittätoista kiloa, moni päälle kuuttakymmentä. Yleisin veikkaus oli 30 kiloa, joka osuu kohtalaisen lähelle oikeaa. Koiran oikea paino on noin 27,5 kiloa — saadut luvut kylläkin pätisivät aikuisempaan ja tukevampaan labradoriin.
Uskoisin, että tulosta selittää epäonnistunut kysymys. Kuva on todella huono: se on vaikeasta perspektiivistä eikä siinä näy muita kohteita, joihin koiran kokoa voisi suhteuttaa — koira näyttää siinä (ainakin minusta) todellista suuremmalta. Kysely saattoikin siis testata enemmän vastaajien kokemusta koirien painosta!
En kuitenkaan ole pettynyt. Hudit kuuluvat tutkimukseen. Tulos osoittaa, että ihmisillä ei ole maagista kollektiivista arviointikykyä, joka toimisi missä tahansa tilanteessa. Tuloksen puute on tulos itsessään, eikä sitä aina arvosteta tarpeeksi. Tarinan opetus: huonoihin kysymyksiin ei ole hyviä vastauksia!
Keskiarvoarvailu
Yleensä tämä peli tunnetaan muodossa "arvaa $\frac{2}{3}$ keskiarvosta", mutta minähän en perinteisestä Alain Ledoux'n muotoilusta välittänyt. (Vinkki itselle: tarkista Wikipedia ennen kyselyn aloittamista.) Peliä on pelattu muutamaan otteeseen isoilla porukoilla ja se on klassinen peliteorian esimerkki.
Pelille on vaikea määrittää hyvää strategiaa. Jos kaikki pelaavat täydellisesti (kuten peliteoriassa usein oletetaan), jokainen vastaa 0 ja voittaa pelin. Vastaajista 33 (eli 22 %) toimi juuri niin. Toisaalta todellisissa peleissä esiintyy pelaajia, jotka eivät noudata täydellistä strategiaa. Meidän kokeilussamme moni vastasi nollaa suuremmalla luvulla. Negatiivisten lukujen salliminen oli kiinnostava kokeilu, mutta luulen sen lähinnä sotkeneen tilannetta — vain kuusi pelaajaa hyödynsi mahdollisuutta.
Keskiarvoksi muodostui 23,74, joten pelin voitti se yksi pelaaja, joka vastasi 24. Onneksi olkoon, oikeakätinen matematiikanvälttelijä!
Kolme vaihtoehtoa
Törmäsin tähän kysymykseen hiljattain Twitter-äänestyksessä, joka onnistui tehtävässä aika mainiosti. Tämä pulma vaatii jonkinlaista strategiaa, koska muiden pelaajien vastaukset eivät ole tiedossa. Jos jokainen yksinkertaistaa sen keskimmäinen/joku muu -kolikonheitoksi, tuloksesta tulee täydellinen.
Meidän tapauksessamme ei käynyt ihan niin. Vaihtoehto A kyllä sai toivotun 24 % tuloksen, mutta B ja C menivät melkein tasan.
Aluksi tämä näytti todella vakuuttavalta. Kun tarkistin tilanteen pari tuntia kyselyn alkamisen jälkeen, ensimmäiset parikymmentä vastaajaa olivat onnistuneet tehtävässä täydellisesti! Iltaan mennessä tulokset olivat jakautuneet harmillisesti tasan, mutta loppua kohden tulos parani jälleen — loppujen lopuksi 39 % vastanneista oli valinnut keskimmäisen vaihtoehdon. Valitse yksi neljästä -tehtävän kolmonen osui siis lähemmäs puolenvälin tavoitetta, mikä on mielestäni aika huvittavaa.
Taustoitus
Ainoa taustakysymys, jonka tarkoituksena oli liittyä aiheeseen, käsitteli matematiikan käyttöä. Noin neljännes vastanneista sanoi työskentelevänsä tai opiskelevansa matematiikan parissa. Viidennes sanoi välttävänsä matematiikkaa kuin ruttoa, ja loput joutuivat/pääsivät käyttämään matematiikkaa jonkun verran töiden tai opintojen parissa. Voisin veikata matematiikanvälttäjiä olevan valtakunnallisella tasolla enemmän.
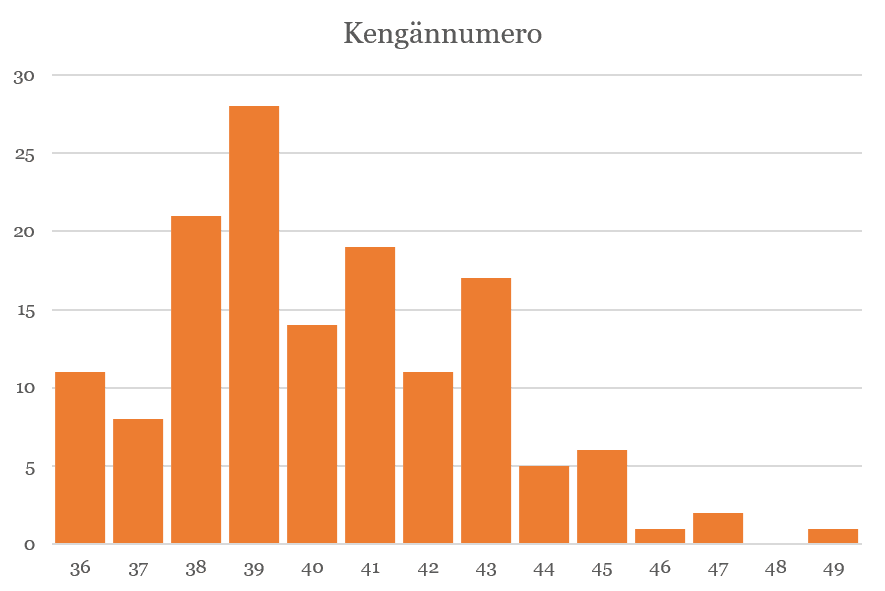
Yllättävänä juttuna kengännumerokysymys säästyi lähes kokonaan kummallisilta vastauksilta — rajasin tästä pois hyvin epäuskottavat vastaukset 4, 8 ja 104. (Pahoittelen, mikäli poistin sinut perusteetta.) Yleisin kengännumero oli 39, keskimääräinen 40,2 ja mediaani 40. Keskihajonta oli 2,7. Tämä jopa vastannee aika hyvin todellisuutta.
Kätisyytensä kertoneista 87 % oli oikeakätisiä, 9 % vasenkätisiä ja loput 4 % molempikätisiä. Nämäkin luvut lienevät samaa luokkaa kuin voisi odottaa.
Päätin jättää taustoitusosion lyhyeksi. Ikä ja sukupuoli ovat kysymyksiä, joiden avulla voisi hyvinkin löytyä kiinnostavia korrelaatioita, mutta ne myös tarkentavat vastaajan henkilökuvaa. Näin epätieteellisessä tutkimuksessa ei ollut mielestäni tarvetta niille tiedoille. Vaikka sopivasta kätisyyden ja kengännumeron yhdistelmästäkin voi tunnistaa tutun, koin riskin siihen sopivan pieneksi. Viimeiset kaksi kysymystä ovat lähinnä mielenkiinnosta, noudattavatko vastaukset todellista jakaumaa. Ne myöskin ovat matikantuntien klassikoita, mutta harvassa luokassa saa näin suurta otosta!
Kokeile itse!
Kerätty aineisto on vapaasti käytettävissä. Rivit on anonymisoitu poistamalla aikaleimat ja sekoittamalla niiden järjestys. Lisenssiksi valitsin Creative Commons Nimeä 4.0 -lisenssin, joka sallii aineiston käytön miten tahansa, kunhan alkuperäinen lähde on mainittu. Lisäksi joukossa on muutama työkalu, joilla käsittelin dataa. Mikäli louhit aineistosta lisää kiinnostavia löytöjä tai käytät sitä jotenkin luovasti, vinkkaa minullekin. (Lisäpisteet jostain aivan hulvattomasta korrelaatiosta.) Pidä hauskaa!
- Kaikki tiedostot
- Anonymisoitu aineisto CSV-muodossa (Lataa selaimen Tallenna nimellä -ominaisuudella)
- Anonymisoitu aineisto Excel-muodossa
Vielä kerran suuri kiitos kaikille osallistuneille! Tämä oli hauska kokeilu!









Ei kommentteja:
Lähetä kommentti
Kommentit ovat moderoituja — yritän hyväksyä kommenttisi mahdollisimman pian. Voit kirjoittaa kommenttiin LaTeX-koodia tai yksinkertaista HTML-merkintää: lue lisää Kommentointi-sivulta.