Erään hakukonehuijauksen anatomia

Yksi päätöksistäni heti bloggaamista aloittaessani oli esiintyä omalla nimelläni ja olla helposti tavoitettavissa. Jos vilkaiset Kuka olen? -sivuani, löydät liudan erilaisia tapoja saada asiasi tietooni. Tämä on ollut pelkästään hyvä päätös, koska sitä kautta olen päässyt kirjoittamaan muuallekin: viimeksi minulla oli suuri kunnia kirjoittaa Fermi-arvioista aineenopettajien Dimensio-lehdessä.

Tällä kertaa en kuitenkaan puhu näistä mahtavista tilaisuuksista. (Joita siis otan mielelläni vastaan!) Sen sijaan puhun siitä yhdestä, josta kieltäydyin. Ja koska tämä on blogi matematiikasta, tähän tarinaan kietoutuu yksi maailman merkittävimmistä algoritmeista. Ja kuten jokaiseen hyvään juttuun, tähänkin liittyy matriiseja.

Vuosi viestien välissä

Lähettäjä: johanna.█████@████████.com
Lähetetty: 17. toukokuuta 2018 19.18
Aihe: Hienot sivut :)

Hei,

Halusin varmistaa, että saitteko viimeistä viestiäni?

Nimeni on siis Johanna ja olisin kiinostunut ostamaan artikkeli -postauksen nettisivultanne. Tarkemmin sanottuna haluaisin julkaista sivustollanne artikkelin/tekstin, joka palvelisi teidän asiakaskuntaa, luoden samalla meidän sivustollemme näkyvyyttä. Edustan muutamaa suomalaista rahapelisivustoa.

Olisiko tämä mahdollista teidän sivustollanne? Mikäli teille herää mitään kysymyksiä, vastaan mielelläni.

Yt,

Johanna ████████

Johanna, mikä hänen oikea nimensä sitten onkaan, ei ollut ensimmäistä kertaa asialla. Edellinen kerta oli lähes tismalleen vuotta aiemmin, ja vaikka muutama lause olikin nyt eri tavalla kirjoitettu, "kiinostunut" oli edelleen yhdellä ännällä.

Vuosi takaperin vastasin suoraan, ettei minua kiinosta. Vastaan joka yhteydenottoon, tässä tapauksessa vähintäänkin spämmääjän aikaa tuhlatakseni. Tämä uusi yritys alkoi tuntua jo niin naurettavalta, että lähetin astetta passiivis-aggressiivisemman ja sarkastisemman vastauksen. Kerroin, kuinka aiemmissa teksteissäni formaatti on ollut osoittaa pelaajan häviävän ja pohtia, miten säännöt kannustavat tappiolliseen pelaamiseen. Tässä tapauksessa kantavia teemoja voisivat olla vaikkapa kate tai hyväuskoisuus.

Se tältä vuodelta, ensi toukokuussa uudestaan, ajattelin. Mutta muutamaa päivää myöhemmin sain uuden viestin:

Hei Petri,

Kiitos vastauksestasi!

Uskon, että saadaan tuo formaatti ehdottomasti toimimaan ja halutaankin pitää artikkeli mahdollisimman luonnollisena.

Kävisikö teille semmoinen asetelma, että kirjoitat artikkelin itse n. 600 sanaa. Tai mikä on luonnollinen määrä sivustollesi. Minä toimitan sinulle meidän kaksi linkkiä ja ankkurit, ja sijoitat ne sitten luonnolisesti tekstiin.

Olisiko sinulla myös jotain ideoita miten voitaisiin yhdistää tämä meidän edustamiin rahapeleihin? Mietin esimerkiksi pokerin, blackjackin tai ruletin kertoimia. Tai vaikka millaiset mahdollisuudet on voittaa nettikasino peleistä.

Voisin tarjota teille tästä 300 euroa, 12 kuukauden sopimuksella. Miltä tämä kuulostaisi?

Yt,

Johanna ████████

Tämähän alkoi muuttua houkuttelevaksi diiliksi: minun pitäisi vain kirjoittaa reilun mittainen blogaus, jossa haukun toistaiseksi tuntemattomat firmat ja heidän asiakkaansa, laittaa siihen pari linkkiä ja ansaitsisin moninkertaisesti aineenopettajalehtiin kirjoitteluun verrattuna! Mikä voisi mennä pieleen?

Lukuunottamatta tietenkin sitä, että kyseessä on ammattitermiä käyttääkseni ns. kusetus, enkä varmasti saisi mitään rahoja yhtään millekään tilille. Mutta mitä Johanna on yrittämässä saavuttaa? Tässä kohtaa kuvaan astuu algoritmi.

Stanford, 90-luvun loppu

Sergey Brin ja Larry Page eivät keksineet hakukonetta. Jo muutaman vuoden ajan alkukantaisessa internetissä oli ollut sivuja, jotka osasivat linkittää hakusanoja vastaaville sivuille. Ongelma vain oli siinä, etteivät hakutulokset olleet kovin hyviä. Nämä kaksi tohtoriopiskelijaa päättivät muuttaa asian, ja siinä he todellakin onnistuivat: algoritmista nimeltä PageRank tuli perusta pienelle autotallifirmalle, jonka nimen löydät vaikkapa googlaamalla.

Hakukoneessa on rajusti yksinkertaistaen kaksi osaa. Ensimmäinen osa on selvittää, mitkä sivut vastaavat hakusanaa. Toinen osa on päättää, mihin järjestykseen ne laitetaan, ja juuri siitä on kyse tässä algoritmissa. Jotta homma pysyisi yksinkertaisena ja seurattavana, jätetään ensimmäinen ongelma jonkun muun ratkottavaksi. Heitetään lisäksi pois kaikki epärelevantti ryönä ja jäljelle jätetään tasan viisi nettisivua. Koska internetin idea on nimenomaan inter-, näiden sivujen välillä on linkkejä, jotka on esitetty kuvan muodossa alla.

Mikä näistä sivuista on kaikkein suosituin ja arvostetuin, jos et tiedä, kuinka monta kävijää kullakin on?

Ei liene kovin kaukaa haettua ajatella, että suosituille sivuille varmaankin linkitetään paljon. Ei myöskään ole ihan typerää ajatella, että sivut linkittävät usein itseään arvostetummille sivuille. Siispä ylimmän sivun täytyy olla arvostettu, koska huippusuosittu kakkonen linkittää sinne. Miten on muiden sivujen laita?

Oletetaan, että sinulla on tylsä päivä ja selailet nettiä päämäärättömästi. Aloitat joltakin sivulta ja etenet aina jotakin kiinnostavaa linkkiä pitkin seuraavalle, kunnes turhaudut ja aloitat uudestaan joltakin satunnaiselta sivulta. Sivun suosio on tällöin todennäköisyys, että satut päätymään sille jossain vaiheessa seikkailuasi. Esimerkkinettimme viitossivulle pääsee vain aloituksen arpaonnella, joten se tuskin on kovin suosittu. Ykkössivu taas on väistämättä muutaman klikkauksen päässä, joten sen täytyy olla hyvä!

(Asian vierestä sanoen, tätä temppua kannattaa kokeilla Wikipediassa: Aloita satunnaisesta artikkelista ja klikkaa aina ensimmäistä linkkiä, joka ei ole sulkeiden sisällä. Minne päädyt lähes joka kerralla?)

Googlen algoritmissa on juurikin kyse tylsistyneestä netinselailijasta, joskin työn huomattavasti nopeammin tekevästä robotista. Heillä on joukko tietokoneita, joiden ainoa tehtävä on ladata nettisivuja ja kirjata ylös, mille sivuille ne linkkaavat. Tämän tiedon pohjalta toinen järjestelmä voi sitten leikkiä satunnaisesti surffailevia ihmisiä ja katsoa, miten todennäköisyyksille käy.

Kirjoitin pienen koodinpätkän, joka teki juuri tämän viisisivuisessa netissämme. Jokaisella sivulla se joko klikkasi satunnaista linkkiä tai 15 % todennäköisyydellä tylsistyi ja hyppäsi satunnaiselle sivulle. Se teki satatuhatta kierrosta ympäri "nettiä" ajassa, jossa sinä ehdit hädin tuskin klikata kissavideota, ja sai tulokseksi seuraavat luvut:

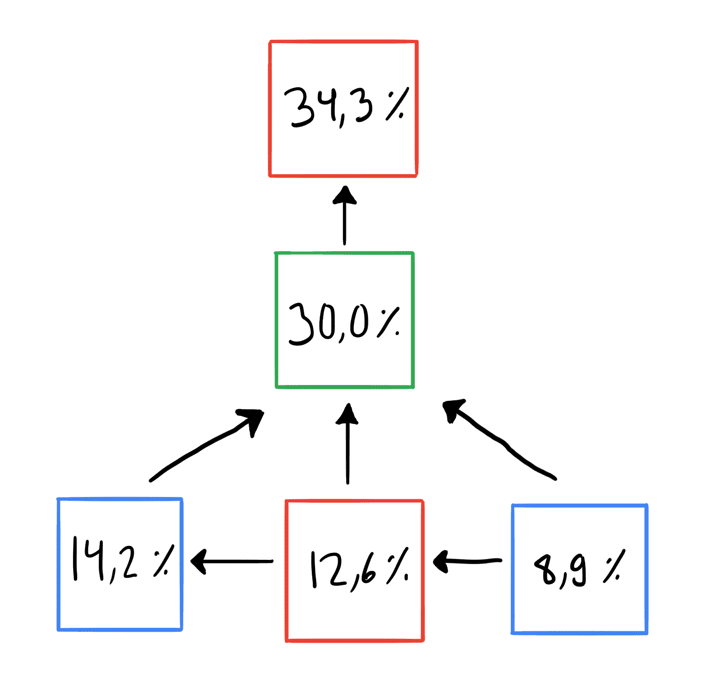
Vaikuttavaa, mutta miten matriisit liittyvät tähän? No, tässä tekniikassa on pieni, muutaman miljardin nettisivun suuruinen pulma. Jotta syrjäisetkin sivut voitaisiin rankata, satunnaisen surffarin täytyisi osua niille useita kertoja — mitä enemmän, sitä tarkempi tuloksesta tulee. Se taas vaatisi vielä useampia miljardeja toistoja, ja se olisi pikkuisen liikaa hakukoneelle, joka ei halua olla vuosikymmentä jäljessä ajastaan.

Matriisi nimeltä $G$

Vedetäänpä siis esiin ihmelääke nimeltä matriisi! Matriisi on lukiosta tutun vektorin yleistys suorakulmaiseksi lukutaulukoksi. Esimerkiksi nämä kaksi ovat matriiseja, ja vasemmanpuoleinen on helppo tulkita vanhaksi tutuksi vektoriksi:

\[ \begin{bmatrix}1 \\ -2 \\ 3\end{bmatrix} \quad \begin{bmatrix} 0.1 & -3.2\\ 1.0 & 7.5 \end{bmatrix} \]

Matriiseja voi laskea yhteen, vähentää ja kertoa reaaliluvuilla arvattavalla tavalla: alkio kerrallaan. Kahden matriisin kertominen keskenään on hieman monimutkaisempaa, sillä kukin tulosalkio riippuu useammasta lähtöalkiosta loogisella mutta nyt ohitettavalla tavalla. (Tämä kertolasku ei esimerkiksi ole vaihdannaista.) Olennaista on se, mitä matriiseja kertomalla saadaan aikaan.

Jos olet lukenut tätä blogia jo viime syksynä, saatat muistaa sadun apteekkarista ja hänen nuoresta apulaisestaan. (Jos et, nyt on hyvä hetki vilkaista!) Tarinassa nuori matemaatikko näytti, kuinka apteekkarin ratkoman pulman saattoi ajatella matriisien avulla ihan eri lailla ja saada helposti uusia tuloksia. Hakukoneen ongelmassa ajattelutavan muutos on ihan välttämätön.

Esitetään viiden sivun verkko vähän eri tavalla. Tässä matriisissa rivit ja sarakkeet kuvaavat eri nettisivuja. Esimerkiksi kolmannella rivillä on sivu numero kolme, ja rivillä makoilevat ykköset tarkoittavat, että sivulla on linkit sivuille kaksi ja neljä.

\[ L = \begin{bmatrix} 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0 & 0\\ 0 & 1 & 0 & 1 & 0 \end{bmatrix}. \]

Tämänkaltainen muunnos verkosta matriisiksi on aika yleinen tietojenkäsittelytieteessä. Tehdään sitten toinen temppu, jossa ykköset korvataan todennäköisyyksillä. Toisella sivulla on vain yksi linkki, joten selailija klikkaa sitä todennäköisyydellä $1$. Kolmannella taas on kaksi linkkiä, joista kummankin todennäköisyys on $0.5$, ja niin edelleen.

\[ H = \begin{bmatrix} 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0.5 & 0.5 & 0 & 0\\ 0 & 0.5 & 0 & 0.5 & 0 \end{bmatrix}. \]

Sitten vielä pitää lisätä tylsistymisen mahdollisuus. Ykkösrivi kuvaa umpikujaa, joten sille saapuva surffailija valitsee täysin umpimähkään uuden kohteen, jonka todennäköisyys on tällöin $1/5$. Muilla riveillä taas luvut kerrotaan termillä $0.85$ ja lisätään $0.15 \times 1/5$, joka kuvaa satunnaisen sivun valintaa 15 % todennäköisyydellä. Lopputuloksena on matriisi

\[ G = \begin{bmatrix} 0.2 & 0.2 & 0.2 & 0.2 & 0.2\\ 0.88 & 0.03 & 0.03 & 0.03 & 0.03\\ 0.03 & 0.88 & 0.03 & 0.03 & 0.03\\ 0.03 & 0.455 & 0.455 & 0.03 & 0.03\\ 0.03 & 0.455 & 0.03 & 0.455 & 0.03 \end{bmatrix}. \]

Tämän matriisin nimi on $G$ niin kuin Google, ja sillä sattuu olemaan muutama kiinnostava ominaisuus. Huomaat varmaan heti, että jokainen alkio on nollaa suurempi. Lisäksi jokaisen rivin alkiot summautuvat tasan tarkkaan ykköseksi. Tämäntyyppisiä matriiseja kutsutaan stokastisiksi matriiseiksi, koska sellaisia ilmenee stokastisten eli satunnaisten prosessien tutkimuksessa.

Yksi tärkeä ominaisuus on, että kahden stokastisen matriisin tulo on niin ikään stokastinen. Toinen tärkeä ominaisuus on kyseisen matriisin eräs ominaisvektori. Sattuu olemaan niin, että jokaisella stokastista matriisia vastaa vektori, nimeltään vaikkapa $p$, jota kyseisellä matriisilla kertominen ei muuta. Toisin sanoen $pG = p$. Esimerkin matriisin tapauksessa tämän vektorin likiarvo on

\[ p \approx \begin{bmatrix} 0.344& 0.300& 0.142& 0.126& 0.088 \end{bmatrix}. \]

Saatat havaita, että näissä luvuissa on jotain tuttua. Satunnainen surffailija onkin stokastinen matriisi!

Pienelle esimerkille ominaisvektorin laskeminen on helppoa — vaikkakin käsipelillä kohtalaisen tylsää — mutta monen miljardin nettisivun kohdalla tehtävä on käytännössä mahdoton. Stokastisilla matriiseilla on kuitenkin vielä yksi hauska ominaisuus. Sattuu nimittäin olemaan niin, että

\[ p \approx \begin{bmatrix}0.2 & 0.2 & 0.2 & 0.2 & 0.2\end{bmatrix} G^n \]

jollekin tarpeeksi isolle luvulle $n$, eli ratkaisun saa ihan vain kertolaskujen avulla. Viiden sivun verkon tapauksessa "tarpeeksi iso" $n$ on $5$. Koko internetin tapauksessa "tarpeeksi iso" on ehkä $50$. Ja se ei ole enää niin paljon se! Asiaa helpottaa huomattavasti vielä se, että pienellä jumppaamisella samanlaisen tuloksen saa johdettua matriisista $H$, joka koostuu lähes kokonaan nollista — ja kaikkihan tietävät, miten helppoa nollalla kertominen on!

Näin siis matriisi mahdollistaa verkkosivujen paremmuusjärjestyksen. Parin vuosikymmenen varrella Google on toki hienosäätänyt algoritmia runsaasti. Algoritmi osaa ottaa huomioon sivujen rakenteen, kielen ja satoja muita parametreja, joista kaikista varmaan firma itsekään ei ole täysin perillä. Varmaa on se, että Google on pumpannut siihen valtavasti rahaa, ja hyvästä syystä.

Netin pimeä nurkka

Eräässä artikkelissaan vuosituhannen vaihteelta Brin ja Page esittelevät projektinsa rakennetta. Paitsi että artikkelissa on kiinnostavia lukuja aikakauden netin koosta — Googlen tarvitsema data kattoi silloin massiiviset 50 gigatavua! — ja kuvausta teknisistä ratkaisuista järjestelmän skaalaamiseen, se myös sisältää hauskan kommentin mainonnan ja hakukoneiden suhteesta. Pientä, irrallista palasta liitteestä A vapaasti suomentaen:

[...] odotamme, että mainonnalla rahoitetut hakukoneet tulevat luonnostaan olemaan kallellaan mainostajiin päin, pois kuluttajien tarpeista. [...] Uskomme mainonnan aiheuttavan niin paljon eturistiriitoja, että kilpailukykyisen, läpinäkyvän ja akateemisen hakukoneen olemassaolo on olennaista.

Tämä maailman suurimman mainosimperiumin perustajien suusta!

Vakavammin ottaen, kyseisessä liitteessä kehittäjät tiesivät jo, kuinka arvokasta yritykselle on olla hakutulosten kärjessä. Ei vaadi suurta ihmislajin tuntemusta arvatakseen, että tällaista systeemiä alettaisiin hyväksikäyttämään aivan välittömästi. Vaikka Googlen algoritmi oli nerokas, siinä oli puutteensa.

Se ei nimittäin osannut lukea. Se ei tiennyt, onko linkki myönteinen vai kielteinen, tai onko se alkuunkaan ihmisen kirjoittama. Tilastollisesti useimmat linkit ovat suosituksia, joten sillä oletuksella on kohtalaisen hyvä edetä sokeasti.

Eipä siis aikaakaan, kun mainostajat keksivät ovelan tempun: Tuotetaan kasapäin sivuja, jotka pursuavat avainsanoja. Nämä sivut linkittävät toinen toisiinsa, joten algoritmin näkökulmasta ne ovat suosittuja. Lopuksi nämä sivut linkittävät kohteeseen, joka siis saa kunnon boostin näkyvyydelleen hakutuloksissa. Eiväthän tuhannet linkittäjät voi olla väärässä!

Lienee sanomattakin selvää, että linkkifarmaus ei toimi nykyään niin hyvin. Lienee niin ikään sanomattakin selvää, että hämärät markkinoijat keksivät yhä uusia tapoja kiertää hakukoneiden pelisääntöjä. Dilemma on siinä, missä menee tasapaino luonnollisen sisällön, hyvän kohdentamisen ja epärehellisen mainonnan välillä.

Luonnolliselle tekstille Google ei voi oikein mitään, vaikka heidän ohjeensa muodollisesti kieltävätkin linkkien myymisen. Jos tarpeeksi moni sivu ohimennen viittaa johonkin tuotteeseen, hakukoneen on käytännössä pakko päätellä tuotteen olevan suosittu. Tätä palvelua Johannan yritys kaupittelee täysin avoimesti.

Nollakohdan tapauksessa vaikutus ei olisi edes täysin pieni. Sanon suoraan, että blogiksi tämä on aivan mitätön ja näkymätön. Mutta kuten totesin, olen kirjoittanut muutamaan otteeseen rahapeleistä. Se on täysin tarkoituksellista. Minäkin nimittäin yritän harrastaa hakukoneoptimointia, mutta sanan positiivisessa merkityksessä!

Kokeile googlata "kannattaako Kaikki tai ei mitään" tai "kannattaako Loton tuplaus". Jopa geneerisempi "Kaikki tai ei mitään" tuo aika usein tekstini hakutulosten ykkössivulle. Kaiken kaikkiaan minut nähdään Googlessa muutaman tuhatta kertaa viikossa. Halusin tai en, olen jonkinasteinen auktoriteetti rahapeliasioissa — ja siksi todellakin linkki Nollakohdassa olisi rahanarvoinen. Ei kolmensadan euron, mutta muutaman kuitenkin.

Johannan tavoite ei ollut saada minulta tekstiä, joka houkuttelisi ihmisiä rahapelisivustoille. Voinet hyvin uskoa, ettei minun kirjoittajanlahjoillani muuteta pastaa kullaksi. Mutta Google ei tiedä sitä. Se näkisi vain, kuinka rahapeliauktoriteetin sivulla on suositus.

Toistaiseksi viimeinen viesti

Vastasin toki Johannalle. Totesin, ettei tarjous kuulosta kovin hyvältä juuri niistä syistä, jotka olen tässä esittänyt. Kerroin myös kirjoittavani aiheesta blogitekstin ja tarjosin mahdollisuutta kommentoida aihetta tai tapausta.

En ole saanut vastausta. Ehkä ensi vuonna kuulemme taas.