Teekkarin ja teoreetikon ylin ystävä

Matemaatikkona olemiseen kuuluu myös kulttuurista tuntemusta kuten alalla olijoiden yhteistä sanastoa. Yksi tärkeimmistä tällaisista sanoista on käsienheiluttelu. Se viittaa siihen, mitä tilastotieteilijät, fyysikot ja teekkarit parhaiten tekevät eli tarkkojen perustelujen sivuuttamiseen.

Vaikka sanaa toki voi käyttää myös loukkauksena, mielestäni käsienheiluttelussa ei ole mitään pahaa. Tosimaailmassa nimenomaan täytyy ohittaa yksityiskohtia ja tehdä valistuneita arvauksia, jos aikoo saada jotain aikaiseksi. Ja joskus käsienheiluttelu johtaa jonkin suuremman äärelle. Tässä tapauksessa se vie syvälle funktioiden ymmärtämiseen tavalla, josta niin diplomi-insinööri kuin akateemikkokin tykkää.

Sinnepäin lukiotyylillä

Pitkän matematiikan kurssilla numero kaksitoista opitaan semmoinen epeli kuin Taylorin summa. Sen avulla voidaan approksimoida vaikeitakin funktioita tavallisten, helposti laskettavien polynomien avulla. Brook Taylorin fiksu idea (puhelinnumero 1685–1731, maakoodi Englanti) oli, että jonkin pisteen lähellä funktiota voi arvioida derivaatan avulla, ja derivaattaa toisen derivaatan avulla, ja niin edelleen.

Nykäistään esiin vaikka vanha kunnon sinifunktio, tuo loputon aaltoilija. Tunnetusti (YKSIKKÖYMPYRÄ! huudahtaisi lukioaikainen matikanopeni) $\sin 0 = 0$. Otetaan se ensimmäiseksi arvaukseksi vakiofunktion $f_0(x) = 0$ muodossa. Kuvasta näkee hyvin, että nollan ympäristössä vaakasuora viiva on lähellä oikeaa sinifunktiota, mutta sitten polut erkanevat (sinin tapauksessa yhtyäkseen jälleen).

Mutta mehän tiedämme, että sinin derivaatta on kosini ja että $\cos 0 = 1$. Koska derivaatta tarkoittaa funktion tangenttia, ei ole kaukaa haettua ajatella, että tangentin piirtämällä saisi paremman arvauksen. Valitaan seuraavaksi arvaukseksi siis $f_1(x) = 0 + 1 \cdot x$. Tämä on nollan ympärillä paljon edellistä parempi, mutta etäämmällä homma huononee.

Eihän se derivaatta tietenkään ole vakio. Voimme tehdä samanlaisen arvion derivaatalle itselleen. Kosinin derivaatta on $-\sin$, joka on taas nollaa nollassa, ja tämän derivaatta edelleen on $-\cos$. Kolmanneksi arvaukseksi saadaan siis \[ f_3(x) = 0 + x + \frac{0 \cdot x^2}{2!} + \frac{-1 \cdot x^3}{3!} = x - \frac{x^3}{6}. \]

Nimittäjään yllättäen ilmestyneet kertomat ($3! = 3 \cdot 2 \cdot 1$) tarvittiin siihen, että korkeampien derivaattojen vaikutukset eivät räjähdä ihan käsiin. Ne itse asiassa olivat paikalla jo aiemminkin, mutta $0! = 1! = 1$ määritelmän mukaan. (Kyllä, $0! = 1$, ja siinä on järkeä.) Tulos näyttää tältä:

Koko ajan vain paranee, ainakaan jos ei katsota kovin kauaksi nollasta. Näyttäisi siltä, että derivaattojen lisääminen laajentaa suht tarkkaa aluetta koko ajan laajemmaksi. Kymmenen termin kohdalla tarkkuus alkaa olla jo melkoisen loistava:

Tällä tavoin voi siis laskea enemmän tai vähemmän hyviä likiarvoja vaikeillekin funktioille. Tämän soveltavaa teekkaria miellyttävän ominaisuuden lisäksi paatunein teoreetikkokin ilahtuu. Sinin kohdalla sattuu nimittäin olemaan niin, että jos summa muutetaan sarjaksi eli kasvatetaan äärettömän pitkäksi, niin saadaan täsmälleen oikea funktio. On siis mahdollista kirjoittaa yhtäsuuruusmerkki kaavaan \[ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots. \]

Tämä temppu ei kelpaa kaikille funktioille (eikä vain siksi, että funktio ei välttämättä derivoidu äärettömän montaa kertaa), mutta toimiessaan se on uskomattoman tehokas. Lukiossa siitä tiedosta ei ole pahemmin hyötyä, mutta yliopistotason analyysissa asia on toinen.

Yksi esimerkki liittyy differentiaaliyhtälöihin. Differentiaaliyhtälössä ei ratkaista tuntematonta muuttujaa vaan tuntematonta funktiota. Esimerkiksi $f'(x) = 2f(x)$ on differentiaaliyhtälö, jonka yksi ratkaisu on $f(x) = e^{2x}$. (Tämä ei ole ainoa ratkaisu. Mikä on yleinen ratkaisu, ja onko siinä kaikki?)

Sattuu olemaan niin, että Taylorin sarjat ovat sangen kivasti käyttäytyviä. Niitä nimittäin on helppo derivoida; kai nyt, kun ne ovat vain pikkaisen pitkiä polynomeja. Siksipä onkin mahdollista arvata, että ratkaisufunktiolla on sarjaesitys, sijoittaa se yhtälöön, ratkaista ja tunnistaa tuttu funktio. Sinin (ja kosinin) lisäksi muun muassa eksponenttifunktiolla on aika helposti tunnistettava alter ego.

Sinistä asiaa

On yksi temppu muuttaa sini polynomiksi, mutta aivan toinen ja ehkä vielä siistimpi kikka on muuttaa polynomi siniksi. Tässä tapauksessa useammaksi siniksi. Ajatuksesta voi syyttää Joseph Fourieria (1768–1830 Ranska).

Tässä tempussa vaaditaan jaksollinen funktio eli sellainen, joka toistuu täsmälleen samana tasaisin väliajoin. Jakson pituudella ei ole väliä, mutta $2\pi$ tekee kaavoista helppoja. Minusta aika kiva esimerkkifunktio on tällainen matemaatikon näkemys sykekäyrästä:

\[ \begin{cases} (x+\pi)^5, & -\pi \leq x < 0,\\ (x-\pi)^5, & 0 \leq x < \pi. \end{cases} \]

Lukijalle jätetään harjoitustehtäväksi keksiä, miltä tämä näyttää äärettömäksi toistettuna.

Taylorin trikissä laskettiin derivaattoja, Fourier’n tempussa taas pannaan kaksi funktiota pussauskoppiin ja integroidaan. Tässä tapauksessa toinen funktio on kosini tai sini.

Ensimmäisessä vaiheessa lasketaan integraali \[ \frac{1}{2\pi} \int_{-\pi}^\pi f(x) \cos(0x) ~dx. \] Tätä kutsutaan myös keskiarvon ottamiseksi, koska $\cos(0x) = 1$. Integraali tarkoittaa funktion ja x-akselin välisen pinta-alan (joka tosin voi olla myös negatiivinen) laskemista, ja kun tämä jaetaan integrointivälin pituudella, jäljelle jää funktion keskimääräinen “korkeus” x-akselista.

Seuraavaksi tehdään jotain vähän kiinnostavampaa, nimittäin laitetaan $\cos(0x)$:n tilalle $\cos(1x)$. Tällöin saadaan “painotettu” keskiarvo (tämä analogia ei kyllä enää pidä vettä). Sitten tehdään sama $\cos (2x)$:n kanssa ja niin edelleen. Näin saadaan selville, kuinka paljon funktiossa on $2\pi / n$:n välein toistuvaa kuviota. Sama operaatio toistetaan sinin kanssa.

Tällä tavalla saadaan kaksi settiä kertoimia, kutsutaan niitä vaikka nimillä $a_n$ ja $b_n$. Ja nyt — tsädäm! — alkuperäinen funktiomme on likimain

\[ f(x) \approx a_0 + b_0 + a_1 \cos x + b_1 \sin x + a_2 \cos 2x + b_2 \sin 2x + \ldots. \]

Sykekäyrälle kolmen termiparin approksimaatio näyttää tältä:

Kolmenkymmenen termin kohdalla aallot alkavat tasaantua ja aletaan olla jo melkoisen lähellä alkuperäistä funktiota. Ainoana ongelmana epäjatkuvuuskohdassa approksimaatio pyyhkäisee överiksi. Tätä kutsutaan Gibbsin ilmiöksi.

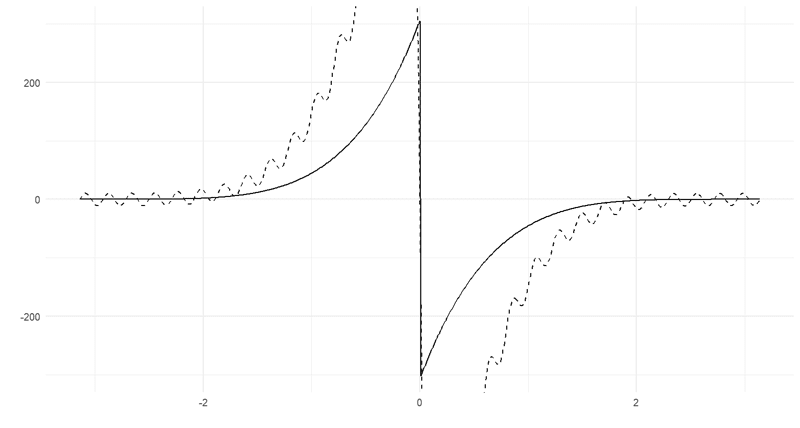
Kuten Taylorin summan tapauksessa, myös Fourier-summa voidaan pidentää äärettömäksi ja saada tarkka esitys. Plussana funktion ei tarvitse tätä varten olla derivoituva, miinuksena sen kuitenkin pitää olla jaksollinen (tai sellaiseksi muunnettava) ja jatkuva toisin kuin esimerkkimme.

Tässä kohtaa ei olisi täysin kohtuutonta kysyä, mitä hyötyä tästä on. Taylorin sarjan avulla pystyi muuttamaan vaikeita funktioita yksinkertaisiksi, mutta Fourier’n temppuhan menee ihan toiseen suuntaan. No, ensinnäkin Fourier-sarjan voi yleistää suht helposti kompleksilukuihin, sillä trigonometria liittyy vahvasti niihin. Tällöin kerroinpari muuttuu yhdeksi setiksi kompleksisia kertoimia. (Myös Taylor-sarjaa voi yleistää, muttei ollenkaan niin sievästi.)

Toisekseen, Fourier kehitti menetelmänsä tutkiessaan osittaisdifferentiaaliyhtälöitä. Ajattele tasoa, jonka päällä kulkee funktio kukkuloina ja laaksoina. Siinä missä yhden muuttujan funktiota derivoidaan vain x-suunnassa, tässä on mahdollisuus tutkia myös y-suuntaisia tangentteja.

Osittaisdifferentiaaliyhtälössä esiintyy siis useampia erilaisia derivaattoja yhdelle tuntemattomalle funktiolle. Vaikka kaikkia tavallisiakaan differentiaaliyhtälöitä ei voi ratkaista suoraan, nämä kaverit ovat jo todella hankalia. Harmi kyllä niitä esiintyy kiitettävän paljon osapuilleen kaikissa fysiikan ongelmissa. Yksi esimerkki on lämmön johtuminen väliaineessa. Fourier tutki nimenomaan niin sanottua lämpöyhtälöä:

Fourier-sarjojen tutkimus on yllättävän iso matematiikan ala. On olemassa muitakin samankaltaisia virityksiä eikä tutkimuksessa tietenkään tarvitse rajoittua tavallisen maailman geometriaan. Helsingin yliopistossakin on useampi professori, joiden erityisalaa tämä on.

Siispä fyysikot rakastavat Fourier’ta ja matemaatikot rakastavat Fourier’ta. Kaiken lisäksi myös teekkarit ovat ihan pihkassa.

Teekkarin ylin ystävä

Jos otat ensimmäisen vastaantulevan teekkarin ja kysyt, onko hän käyttänyt viimeksi deodoranttia vai Matlab-ohjelman fft-komentoa, veikkaan vastauksen olevan sataprosenttisesti jälkimmäinen ainakin signaalinkäsittelyn laitoksella. (Huom. Tietoni teekkareista ovat osittain puutteellisia.)

Jossain ehkä kolmannen vuoden yliopistomatematiikan opintojen kohdalla alkaa käydä ilmi, että loputtomat summat ja integraalit ovat itse asiassa jokseenkin sama asia. Siksi on tietenkin luonnollista kokeilla, miten Fourier-summalle käy, kun $n$ korvataan muuttujalla ja $\sum$ merkillä $\int$.

Otetaan funktio $f(x)$. Se voi olla esimerkiksi lyhyt äänisignaali, tässä tapauksessa erään kappaleen alku. Tällöin muuttuja $x$ tarkoittaa aikaa ja funktion arvo kullakin hetkellä on vallitseva äänenpaine. Ensimmäisen sekunnin aikana kuuluu kolme säveltä, kaikki hieman eri voimakkuuksilla. Lisäksi keskimmäinen sykerö näyttää selvästi tiiviimmältä kuin ensimmäinen, mutta sen tarkemmin on vaikea arvioida sävelten korkeuksia.

Laskemalla hitusen häijy integraali, jota kutsutaan Fourier-muunnokseksi, saadaan funktio $\hat f(t)$. Siinä muuttuja onkin taajuus $t$ ja funktion arvo kertoo, kuinka paljon tätä taajuutta signaalista löytyy! Arvo on kompleksiluku, mutta kompleksiluvut ovat vektoreita ja vektoreilla on pituus, joka kelpaa kuvaajalla esitettäväksi:

Kiinnitä huomiota piikkeihin kuvaajalla. Niitä on kolme kappaletta ja niistä kukin vastaa yhtä säveltä edellisessä kuvassa. Tässä kuvassa ei toisaalta näy ajallista informaatiota, joten jää pääteltäväksi, mikä piikki vastaa mitä biittiä. Nämä kaksi kuvaa esittävät siis saman asian kahdesta hyvin erilaisesta näkökulmasta.

Edellä mainittu fft-komento tulee sanoista Fast Fourier Transform, nopea Fourier-muunnos. Se on laskentamenetelmä, jolla mikä tahansa signaali saadaan purettua taajuuksikseen. Taajuuksista taas on erittäin paljon hyötyä missä tahansa insinööritoiminnassa, ja siksi Fourier-muunnokset ovat ymmärtääkseni olennainen osa teekkarin perusopintoja.

Toinen esimerkki: Valokuvassa taajuuksia on sekä x- että y-suunnissa. Kunkin taajuuden suuruus näkyy oikeanpuoleisessa kuvassa siten, että matalat taajuudet ovat keskellä ja korkeat reunoilla. Matalat taajuudet tuottavat laajoja tasaisia pintoja ja korkeat taas yksityiskohtia ja reunoja. Siksipä kuvaa voi muokata kertomalla taajuuksia jollakin funktiolla. Keskimmäisessä kuvassa on peitetty korkeat taajuudet, alimmaisessa taas vaimennettu matalat ja tehostettu korkeita.

Puhelimesi hyödyntää Fourier-muunnosta aina, kun otat valokuvan tai kuuntelet musiikkia. Jotta tiedostot olisivat riittävän pieniä netin yli siirrettäväksi, niitä pitää pakata. Idea on jakaa ääni tai kuva pieniin palasiin ja nämä palaset edelleen kasaksi kertoimia erään Fourier-summan sukulaisen avulla. Osa näistä kertoimista voidaan tiputtaa tai tallentaa pienemmällä tarkkuudella ilman, että ihminen juuri huomaa eroa. Tärkeintä on, että pääpiirteet pysyvät osapuilleen samoina.

Esimerkiksi tuo edellinen kuvaruudukko oli JPEG-pakattu. Tosiasiassa oikean reunan Fourier-muunnokset näyttävät hieman erilaisilta ilman pakkausta… vai mitä sanot keskimmäisen suurennetusta ja kirkastetusta versiosta? Alkuperäinen on vasemmalla, oikeanpuoleisessa näkyy eroja muun muassa vaalean ja mustan rajalla. (Ja ei, tätä kuvaparia ei ole JPEG-pakattu!)

Näin siis Fourier-muunnos sekä mahdollistaa nykyaikaisen tekniikan että tarjoaa tekemistä teoreetikoille; ei huonommin jutulta, joka sai alkunsa approksimoinnista. Siksi käsienheiluttelusta saa puolestani olla hyvinkin ylpeä!